8 Odd balls
Many times the existing methods are not enough to answer the questions we have. Most of the time, non-parametric statistics are the answer. In this section, we will discuss some of the cases where we had to use non-parametric statistics.
8.1 Non-parametric statistics
Non-parametric statistics are statistical methods in which parametric assumptions such as probability function or model parameters are not made. In other words, non-parametric statistics are distribution-free methods. With many non-parametric methods, simulation-based methods are the most commonly used. The following papers show a couple of examples using non-parametric methods applied to network inference problems.
8.2 Case 1: Social mimicry
In Bell et al. (2019), we investigated the prevalence of social mimicry in families while eating. Social mimicry is a widely studied phenomenon. And while some statistical methods try to measure it, we approach the problem differently. Instead of assuming mimicry and measuring it right away, we started by asking if there was mimicry in the first place.
The study featured an experiment that consisted of the following:
Families were invited to a lab and were asked to eat a meal together.
Using accelerometers, we time-stamped the action of taking a bite.
Data was then cleaned and processed to obtain the time stamps of each bite (verified using video recordings of the event).
The null hypothesis was then: “The sequence of bites for Person i and j are independent (i.e., no mimicry).” To test this hypothesis, we used a permutation test. The test consisted of the following:
For each pair of persons i and j, we calculated the average time gap between their bites.
We then generated a null distribution by shuffling the time blocks of each person, i.e., for each dyad:
For each individual, we computed the sequence of time gaps between bites (time between bites each person took).
Using that sequence, we then simulated a new sequence of bites for each individual, fixing the individual level time gap distribution.
Once shuffled, we then computed the average time gap per dyad.
Finally, we used the generated null distribution to assess the prevalence of social mimicry. The next figure shows the results for one dyad:
8.3 Case 2: Imaginary motifs
In Tanaka and Vega Yon (2024), we study the prevalence of perception-based network motifs. While the ERGM framework would be a natural choice, as a first approach, we used non-parametric tests for hypothesis testing. The rest of this section is a reproduction of the methods section of the paper:
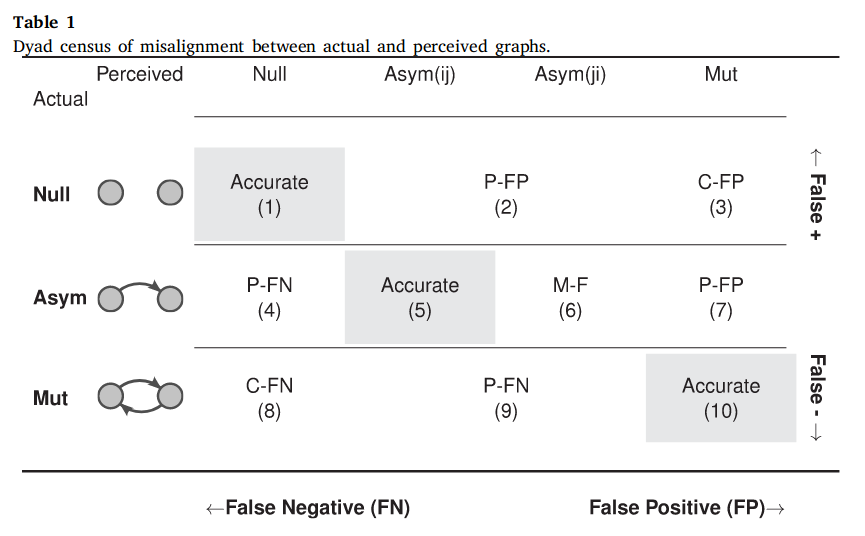
The process can be described as follows:
\begin{equation} \text{Pr}\left(\left.\vphantom{t_{ij} = 1}p_{ij} = 1\right|t_{ij} = 1\right) = \left\{\begin{array}{ll}% |\sum_{\oplus(k)}t_{nm}|^{-1}\sum_{\oplus(k)}p_{nm}t_{nm} &\text{if}\; k \in \{i, j\} \\ |\sum_{\oplus(k)^{\complement}}t_{nm}|^{-1}\sum_{\oplus(k)^\complement}p_{nm}t_{nm} &\text{otherwise}, \end{array}\right. \end{equation}
\begin{equation} \text{Pr}\left(\left.\vphantom{t_{ij} = 0}p_{ij} = 0\right|t_{ij} = 0\right) = \left\{\begin{array}{ll}% |\sum_{\oplus(k)}(1-t_{nm})|^{-1}\sum_{\oplus(k)}(1-p_{nm}t_{nm}) &\text{if}\; k \in \{i, j\} \\ |\sum_{\oplus(k)^{\complement}}(1-t_{nm})|^{-1}\sum_{\oplus(k)^\complement}(1-p_{nm}t_{nm}) &\text{otherwise}, \end{array}\right. \end{equation}
where, \oplus(k) \equiv \left\{(m,n) : (m = k) \oplus (n = k)\right\} is the set of ties involving k, and \oplus(k)^\complement is its complement.
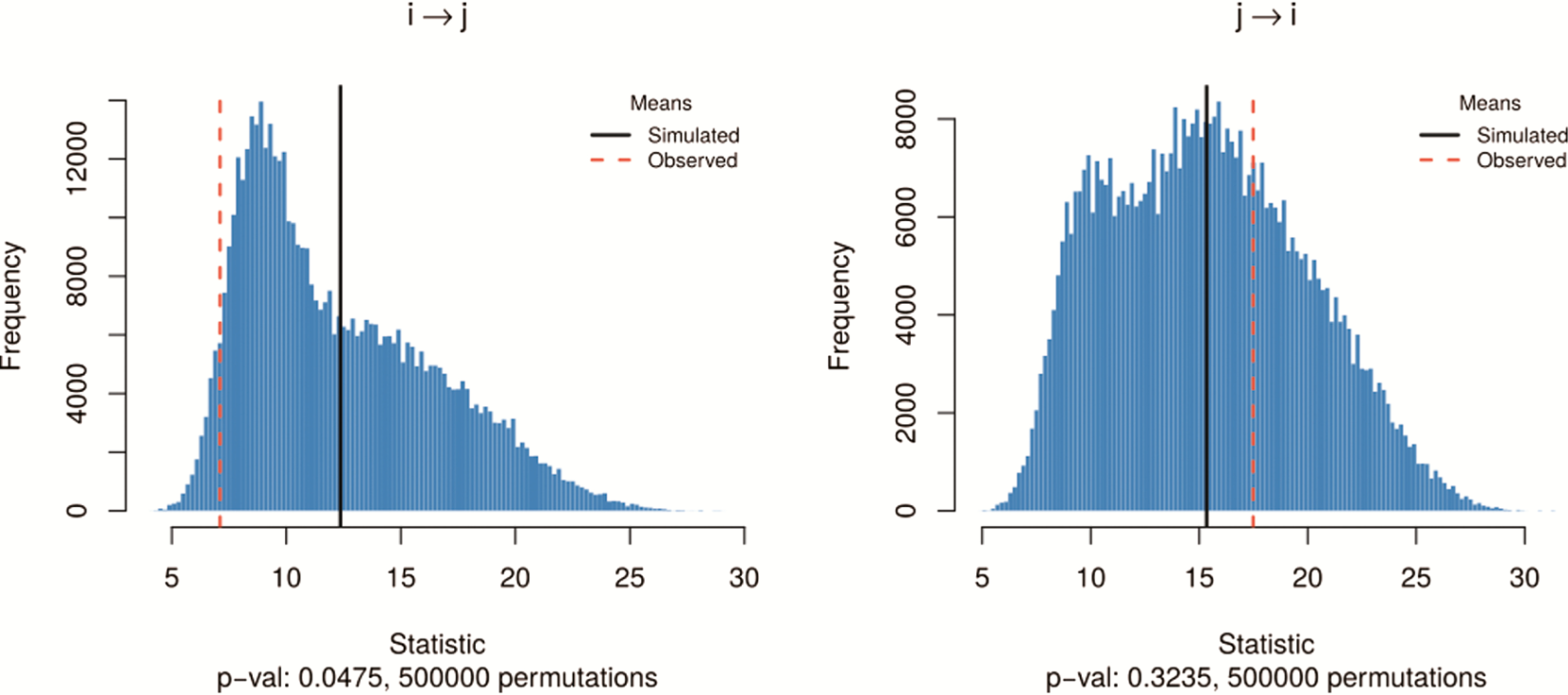
Each sampled perceived graph was \mathbf{P}^b_l–-th sampled graph for each individual . We then counted the dyadic imaginary network motifs, \tau_l^b \equiv s\left(\mathbf{T}, \mathbf{P}^b\right); the same was done to the observed graphs, \hat{\tau}_l \equiv s\left(\mathbf{T}, \mathbf{P}\right). Finally, we calculated a -value using the equal-tail nonparametric test drawing B = 2,000 samples recommend 1,000 minimum) from the null distribution, comparing the observed imaginary motif counts, \hat\tau_l, and what we would expect to see by chance, \{\tau^b_l\}_{b=1}^B:
\begin{equation} \hat{p}(\hat{\tau_l}) = 2\times \min\left[\frac{1}{B}\sum_{b}I(\tau^b_l \leq \hat{\tau_l}), \frac{1}{B}\sum_{b}I(\tau^b_l > \hat{\tau_l})\right] \end{equation}