11  New topics in network modeling

11.1 Overview

  • With more data and computing resources, the things that we can ask and do with networks are becoming increasingly (even more) exciting and complex.

  • In this section, I will introduce some of the latest advancements and forthcoming topics in network modeling.

11.2 Part I: New models and extensions

11.3 Mutli-ERGMs

  • In Krivitsky, Coletti, and Hens (2023a), the authors present a start-to-finish pooled ERGM example featuring heterogeneous data sources.

  • They increase power and allow exploring heterogeneous effects across types/classes of networks.

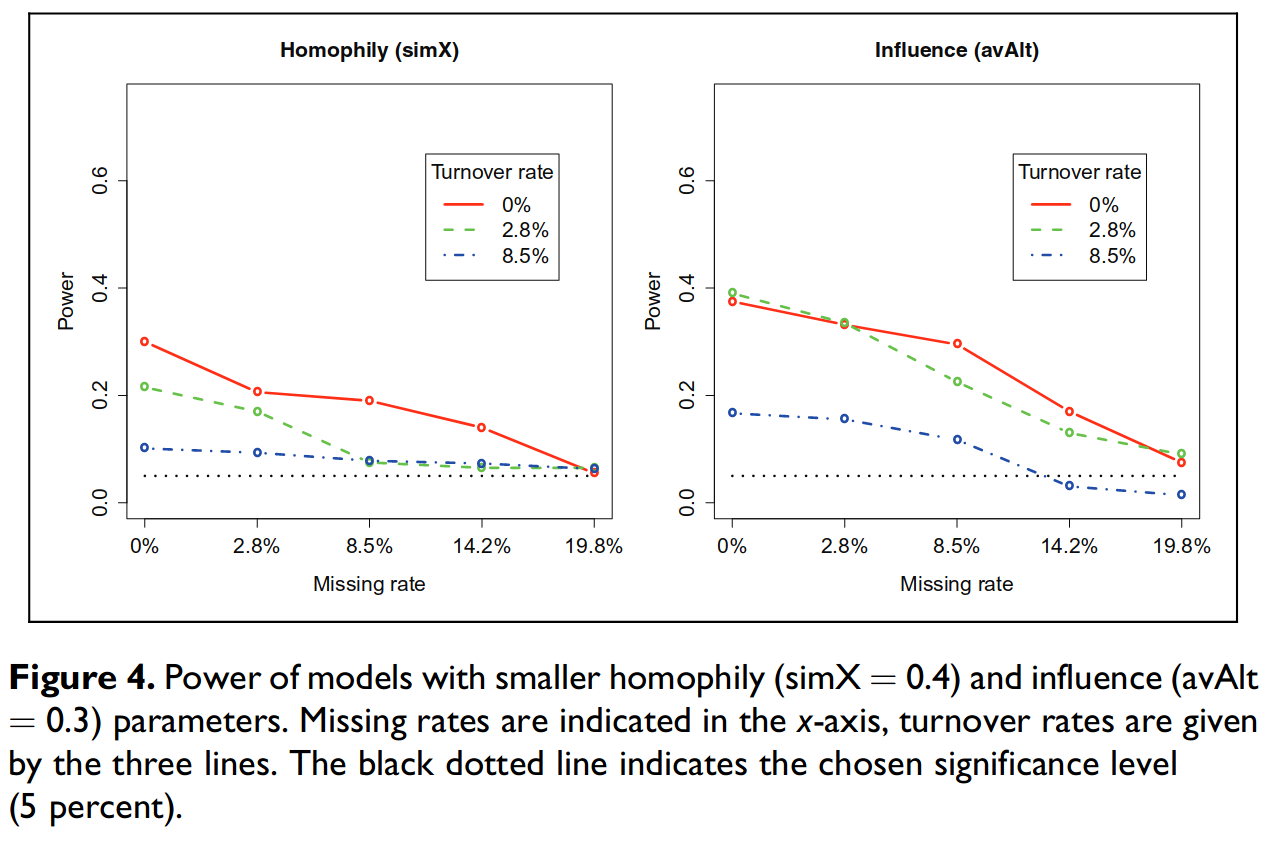
11.4 Statistical power of SOAM

  • SOAM Stadtfeld et al. (2020) proposes ways to perform power analysis for Siena models. At the center of their six-step approach is simulation.

11.5 Bayesian ALAAM

Ever wondered how to model influence exclusively?

  • The Auto-Logistic Actor Attribute Model [ALAAM] is a model that allows us to do just that.

  • Koskinen and Daraganova (2022) extends the ALAAM model to a Bayesian framework.

  • It provides greater flexibility to accommodate more complicated models and add extensions such as hierarchical models.

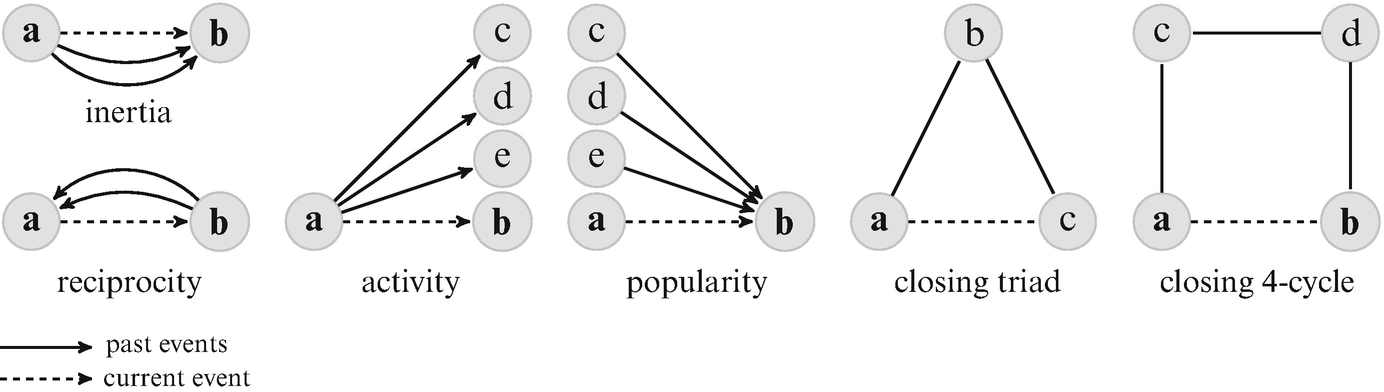
Figure 1 reproduced from A. D. Stivala et al. (2020)

11.6 Relational Event Models

  • REMs are great for modeling sequences of ties (instead of panel or cross-sectional.)

  • Butts et al. (2023) provides a general overview of Relational Event Models [REMs,] new methods, and future steps.

Figure 3 reproduced from Brandenberger (2020)

11.7 Big ERGMs

  • ERGMs In A. Stivala, Robins, and Lomi (2020), a new method is proposed to estimate large ERGMs (featuring millions of nodes).

Partial map of the Internet based on the January 15, 2005 data found on opte.org. – Wiki

11.8 Exponential Random Network Models

  • Wang, Fellows, and Handcock recently published a re-introduction of the ERNM framework (Wang, Fellows, and Handcock 2023).

  • ERNMs generalize ERGMs to incorporate behavior and are the cross-sectional causing of SIENA models.

\begin{align*} \text{ER\textbf{G}M}: & P_{\mathcal{Y}, \bm{{\theta}}}(\bm{{Y}}=\bm{{y}} | \bm{{X}}=\bm{{x}}) \\ \text{ER\textbf{N}M}: & P_{\mathcal{Y}, \bm{{\theta}}}(\bm{{Y}}=\bm{{y}}, \bm{{X}}=\bm{{x}}) \end{align*}

11.9 Part II: Shameless self-promotion

11.10 ERGMitos: Small ERGMs

Five small networks from the ergmito R package

11.11 Discrete Exponential-family Models

  • ERGMs are a particular case of Random Markov fields.

  • We can use the ERGM framework for modeling vectors of binary outcomes, e.g., the consumption of \{tobacco, MJ, alcohol\}

11.12 Power analysis in ERGMs

  • Using conditional ERGMs (closely related to constrained), we can do power analysis for network samples (Vega Yon 2023).

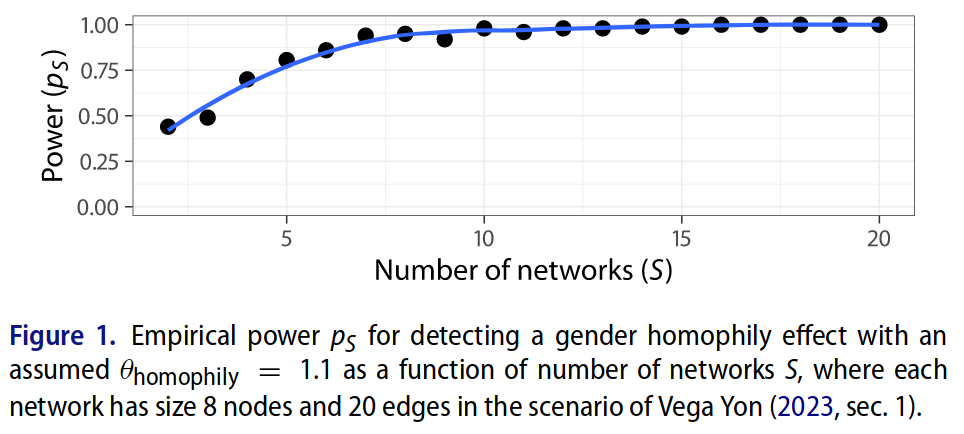
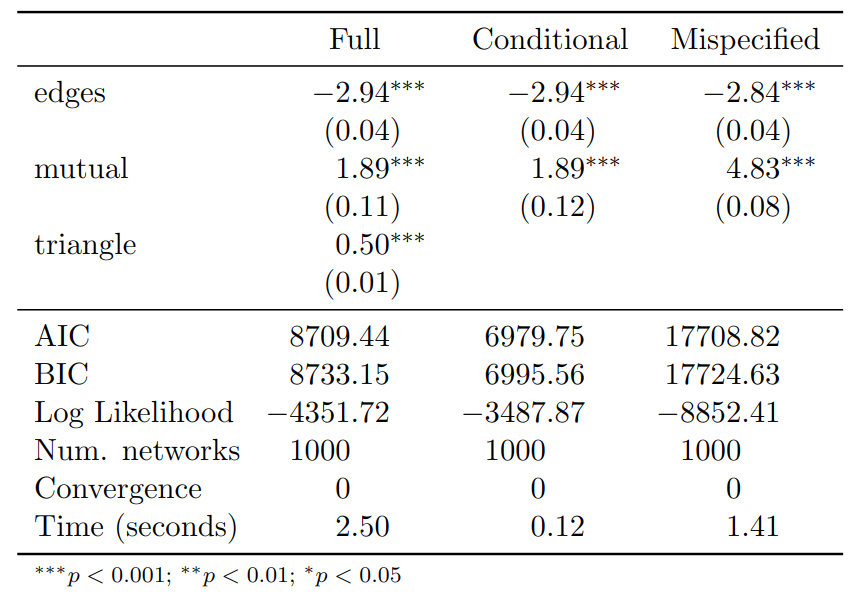
Reproduced from Krivitsky, Coletti, and Hens (2023b)

11.13 Two-step estimation ERGMs

  • Conditioning the ERGM on an observed statistic “drops” the associated coefficient.

  • Hypothesis: As n increases, conditional ERGM estimates are consistent with the full model:

Simulation study trying to demonstrate the concept (Work in progress)

11.14 Thanks!

11.15 Bonus track: Why network scientists don’t use ERGMs?

Attempts to overcome these problems by extending the blockmodel have focused particularly on the use of (more complicated) p^* or exponential random graph models, but while these are conceptually appealing, they quickly lose the analytic tractability of the original blockmodel as their complexity increases.

– Karrer and Newman (2011)

  1. From the Spanish suffix meaning small.↩︎